Paul Lévy. Un témoignage sur le rêve. Extrait de la « Revue de Métaphysique et de Morale », (Paris), 51e année, n°2, avril 1956, pp. 166-173.
Paul Pierre Lévy (1886-1971). Mathématicien, un des initiateurs de la théorie des probabilités.
[p. 166]
UN TÉMOIGNAGE SUR LE RÊVE
1. Il m’est arrivé récemment de penser, en rêve, à une courbe, dont la définition n’est pas du tout élémentaire, et à laquelle je n’avais jamais pensé auparavant. Je ne croyais pas à la possibilité d’un rêve mathématique aussi complexe ; je pense donc, en le racontant, apporter un témoignage utile à l’étude des rêves.
Très souvent, mes rêves sont une suite de sensations si vagues et si peu coordonnées que, lorsque je me les rappelle après le réveil, il m’est impossible de les raconter sans les déformer complètement. Cette imprécision du rêve me paraît augmenter avec l’âge. Toutefois il m’arrive encore assez souvent d’avoir des rêves assez précis, et même de me souvenir au réveil des raisonnements corrects toujours très simples, faits en rêve. Ces raisonnements se présentent par hasard à mon esprit, et ne sont jamais le résultat d’un effort conscient. Le rêve que je vais raconter, tout en dépassant beaucoup par sa complexité tous ceux que j’avais faits antérieurement, a eu aussi le caractère d’une idée qui s’est présentée tout à coup à mon esprit. Je m’excuse si, pour l’exposer, et distinguer l’idée nouvelle de ce qui m’était familier, je suis obligé de faire un petit cours de géométrie, avec figures.
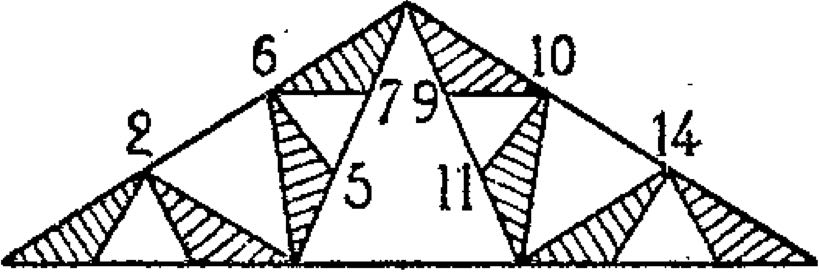2. Il faut d’abord que je définisse la « courbe de von Koch ». C’est une courbe infiniment sinueuse, dont on peut avoir une idée en traçant une suite de lignes polygonales qui s’en rapprochent de plus en plus. J’ai figuré ci-contre (fig. 1), la cinquième approximation, obtenue en parcourant dans l’ordre les dix-sept points numérotés 0 à 16 ; en les parcourant de deux en deux, de quatre en quatre, de huit en huit, ou enfin en allant directement du premier [p. 167] au dernier, on a, en remontant, les quatre premières approximations. En les regardant maintenant dans l’ordre normal, le lecteur verra que chaque approximation est déduite de la précédente par une même construction géométrique : on remplace chaque côté par une ligne semblable à la ligne 0-8-16, et placée de manière à obtenir une ligne qui soit toujours entre les deux lignes précédemment tracées. Ainsi la quatrième ligne et la cinquième comprennent entre elles une chaîne de huit triangles, hachurés sur la figure, dont la courbe ne peut pas sortir. On peut dire qu’elle représente la courbe, tracée avec une plume très grossière. Le tracé des approximations suivantes nécessiterait une plume plus fine. Avec une plume infiniment fine, on pourrait tracer la courbe elle-même.
En modifiant la figure initiale, mais en s’inspirant de l’idée d’une même construction indéfiniment répétée, on obtient des courbes ayant certaines analogies avec celle de von Koch, et ayant comme elle ; la propriété suivante : chacune de ces courbes est composée de parties semblables à la courbe entière. Le mode de définition de ces courbes étant connu une fois pour toutes, il suffit de voir une certaine figure initiale pour savoir que, du moins moyennant certaines conditions, on en déduit une courbe analogue à celle de von Koch.
Au point de vue psychologique, il peut être utile de dire que je suis depuis longtemps familiarisé avec ces courbes ; j’avais étudié la première, à l’âge de seize, ans, indépendamment de von Koch.
Mes travaux m’y ont souvent ramené, et j’ai consacré il y a quelques années un long, mémoire à la catégorie générale des courbes dont je viens de parler. Mais il y avait plusieurs mois que je ne m’en étais pas occupé lorsque je fis le rêve que je vais maintenant raconter.
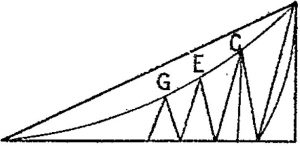3. Il comprit deux parties distinctes. Je peux résumer la première en disant que la figure qui m’apparut tout à coup est la figure ci-contre (fig. 2), où OA est la première approximation d’une certaine ligne, « à la von Koch « , tandis que la seconde est une ligne à une infinité de côtés ABCDEF,GH…, les sommets ACEG… étant sur une courbe OA tangente en 0 à [p. 168] OK (1). Pour passer à l’approximation suivante, on remplacerait AB par une certaine ligne intérieure au triangle ABK et extérieure à une courbe AB tangente à AK ; de même BC par une ligne intérieure au triangle BCL ; et ainsi de suite.
Dans la première partie de mon rêve, j’avais imaginé que les côtés successifs de la ligne ASCD… avaient des pentes croissantes, ce qui n’empêchait pas cette ligne d’aboutir en O en y admettant la tangente OK. Il en est de même de la courbe infiniment sinueuse obtenue comme limite des approximations.
Observant donc, en rêve, cette figure, je vis nettement les deux propriétés suivantes de la courbe qui s’en déduit :
1° Elle admet une infinité de points de rebroussement (notamment’ C, E, G,…) constituant un ensemble partout dense (c’est à-dire que chaque arc de courbe, si petit soit-il, en contient une infinité).
2° Les tangentes de rebroussement sont toutes horizontales ou verticales.
La courbe m’apparut d’ailleurs comme pour me permettre de répondre à une question qui venait de m’être posée par un jeune mathématicien ; du moins j’avais l’impression qu’il venait de me demander quelque chose et que la première de ces propriétés répondait à cette question ; la seconde propriété m’apparut presque aussitôt. Je pense que le tout n’avait duré que quelques secondes.
4. A ce moment je crus me réveiller. Il m’arrive souvent de tomber d’un rêve dans un autre en éprouvant une impression analogue à celle du réveil. Sans doute cela provient-il d’un bruit extérieur qui tend à me réveiller, mais le sommeil est trop profond pour que le réveil soit complet. J’ai alors la sensation exacte de la position de mon corps, je me sens dans un lit, avec l’impression de me réveiller, mais dans une ambiance qui reste plus ou moins celle de mon précédent rêve. C’est ce qui m’arriva alors, et, dans ce nouveau rêve, mes sensations furent les suivantes :
1° D’abord je m’étonnai de mon premier rêve ;
2° Je substituai à la figure décrite une figure analogue, mais où les côtés successifs de la ligne polygonale ABC… ont tous la même pente, cette pente étant complémentaire de celle-de OA, et [p. 169] j’observai que dans ces conditions il s’agissait d’une courbe composée de parties semblables à la courbe entière, courbes rentrant dans la catégorie que j’avais étudiée :
3° Je pensai à une autre courbe possible, qui serait à la précédente ce qu’est à celle de von Koch la courbe (également de von Koch) définie dans le traité d’analyse de M. Émile Picard, et qui est représentable par une équation y = f (x) ; mais cela sans définition précise de cette nouvelle courbe.
4° Je pensai que l’ensemble ferait un mémoire mathématique d’une certaine importance ? et que, pour le rédiger avant le concours d’admission à l’Ecole Polytechnique, dont je devais m’occuper, je me verrais contraint d’abandonner un autre travail auquel j’attachais de l’importante.
A ce moment je m’éveillai complètement. L’ensemble des deux rêves m’apparut comme une suite de sensations très nettes et très brèves, et je suis persuadé qu’en tout il n’avait pas duré une minute.
II
1. Je voudrais maintenant ajouter quelques réflexions sur la rapidité des rêves. Je suis persuadé que l’opinion généralement admise sur ce sujet repose sur une interprétation inexacte des faits : d’après moi, le rêve est rapide, comme-la pensée peut l’être, mais une seconde de temps vécu en rêve ne paraît ni plus ni moins longue que si l’on est éveillé. Je veux d’abord indiquer un argument que je crois décisif en faveur de cette thèse. J’expliquerai ensuite l’origine de l’illusion qui a fait souvent admettre la thèse contraire.
Cet argument est tiré de l’analyse des sensations que l’on éprouve quand on est réveillé par un bruit cadencé, que l’on entendait en rêve, mais en l’interprétant inexactement ; au moment du réveil, la cadence ne change pas. Or, si le bruit se répète par exemple de seconde en seconda et si le rêve est seulement deux fois plus rapide que la réalité, c’est-à-dire si pendant un temps qui a duré réellement une seconde l’homme qui rêve croit en avoir vécu deux, le bruit, en rêve, paraîtrait se reproduire seulement toutes les deux secondes, et, au réveil, la cadence semblerait [p. 170] s’accélérer brusquement. J’ai bien souvent, pour ma part, constaté qu’il n’en est rien.
Bergson a raconté avoir été un jour réveillé par les aboiements d’un chien, qui lui faisaient l’effet de cris poussés par son auditoire au cours d’une conférence. Si la cadence de ce bruit avait changé au réveil, il s’en serait certainement aperçu et l’aurait mentionné dans son récit. Le fait qu’il ne l’ait pas fait constitue donc un témoignage en faveur de la thèse que je soutiens.
Un autre argument est d’ordre physiologique : si nous avons une sensation intérieure de la mesure du temps, c’est sans doute que nous avons en nous « un pendule qui bat la seconde » ; sans doute s’agit-il des vibrations naturelles de certaines molécules cérébrales. On ne conçoit pas que le sommeil puisse accélérer ces vibrations.
On a parfois, en rêve, l’impression de glisser sur le sol, et d’avancer ainsi beaucoup plus vite qu’on ne ferait en réalité. On a cette impression parce qu’on a peut-être cru faire dix mètres en une seconde. Il serait absurde d’en conclure que c’est, en une demi-seconde, ou même moins encore, qu’on a cru faire ces dix mètres ; je pense au contraire que l’idée de Bergson, d’après laquelle une seconde semble toujours être une seconde, s’applique même pendant le rêve (2).
2. Je prie maintenant le lecteur de faire un effort de pensée pour s’imaginer qu’il parcoure un chemin connu, que, par exemple il remonte les Champs-Élysées ; qu’il voie devant lui l’Arc de Triomphe et le fasse peu à peu grandir dans sa pensée, et qu’il fasse défiler en imagination les maisons qui bordent l’avenue. Il lui sera impossible de remonter l’avenue en pensée aussi lentement qu’il le ferait en réalité ; sans s’imaginer qu’il coure, il aura peut-être été en moins d’une minute du Rond-Point jusqu’à l’Étoile.
C’est ce qui se passe en rêve. Si je rêve que je suis les Champs-Élysées vers la place de l’Étoile, la cadence de mes pas sera sans doute celle de ma marche normale. Mais je n’évoquerai pas, dans [p. 171] mon rêve, tous les détails du chemin ; sans doute ne penserai-je même pas aux maisons qui bordent l’avenue, et ne verrai-je que l’Arc de Triomphe, qui grandira à mes yeux beaucoup plus vite qu’il ne ferait en réalité, Chacun des mètres du chemin sur lequel je n’aurai pas fixé ma pensée n’aura pas existé dans mon rêve, et je me trouverai arriver au but après une centaine de pas, ou même moins.
Des circonstances de ce genre sont très fréquentes dans les rêves, qui sont, comme le cinéma, des suites d’images plus ou moins bien reliées. Si ces images sont extraites d’un film cohérent, et se succèdent dans l’ordre normal, on ne s’aperçoit pas qu’il en manque un grand nombre. Au réveil, on a par exemple l’impression d’avoir parcouru un long chemin parce que votre mémoire vous en a montré trois ou quatre des aspects les plus caractéristiques, et notamment les tournants ; à chaque tournant on voit le tournant suivant, et parce que la pensée est tendue vers ce nouveau point on s’y trouve presque aussitôt transporté, en oubliant le parcours intermédiaire… Ainsi, comme, enfant, je traversais chaque jour le Luxembourg pour me rendre au lycée, et je le traversais souvent aussi en rêve ; le souvenir, de mon rêve, au réveil, ne me montrait jamais que trois ou quatre aspects du chemin, toujours les mêmes, et j’avais l’impression d’avoir traversé le Luxembourg en quelques instants.
Des circonstances analogues doivent se produire dans les cas où, pendant un bref sommeil, on croit avoir vécu toute une suite d’aventures compliquées. En réalité on a dû voir, comme au cinéma, une succession de brèves images, dont on a composé une histoire sans s’apercevoir que les images intermédiaires à l’aide desquelles on les enchaîne n’avaient pas existé.
J’ai d’ailleurs souvent constaté, en analysant au réveil le souvenir d’un rêve, des phénomènes qui expliquent cette illusion. Ainsi, je vois arriver en rêve une personne inconnue de moi ; un instant après, sans savoir comment cela se produit, je me trouve connaître certaines particularités de sa vie passée, comme s’il s’agissait d’une personne connue dont le passé peut se présenter à mon esprit quand je la rencontre. Une analyse superficielle du rêve aurait pu me faire croire qu’on m’avait raconté toute une histoire sur cette personne ; il n’en était rien. De nombreuses observations analogues m’ont persuadé qu’on peut, au cours d’un [p. 172] rêve, croire qu’on se souvient d’un rêve antérieur ; et que pourtant ce rêve antérieur n’ait pas eu lieu. On peut ainsi s’expliquer que quelques brèves images, complétées par de faux souvenirs et mal analysées au réveil, donnent l’impression d’une longue histoire, sans que les images réellement perçues, soient plus nombreuses que celles qui peuvent se présenter en quelques instants à la pensée d’un homme éveillé.
C’est en tout cas ce qui a eu lieu pour le rêve que rai raconté tout à l’heure. Il ne comportait pas un grand nombre d’impressions différentes, assez grand pour que je me sois étonné si je les avais eues à l’état de veille ; j’ai eu parfois, étant éveillé, l’impression de découvertes faites d’une manière plus instantanée encore. Ce qui m’a paru digne d’être rapporté ; c’est que cela ait été possible en rêve.
III
En relisant les lignes qui précèdent, écrites il y a un peu plus de cinq ans, je crois devoir signaler un phénomène assez surprenant, et dont les soucis de ces cinq années de guerre, qui m’ont empêché de repenser à mes rêves passés, ne sont certainement pas la seule explication : il ne me restait aucun souvenir du rêve mathématique qu’on vient de lire. Il était si bien effacé de ma mémoire que, répondant il y a quelques jours à un questionnaire de M. Hadamard, je contestais la possibilité de faire en rêve des découvertes scientifiques. C’est tout au plus si, en cherchant maintenant à interroger mes souvenirs, je me rappelle vaguement avoir envoyé à Léon Brunschvicg le récit d’un rêve qui m’avait surpris.
Je ne peux d’ailleurs pas mettre en doute mon propre témoignage. Le manuscrit, qui est sous mes yeux, est bien de moi. Je reconnais trop mes idées familières pour penser que quelqu’un d’autre que moi ait pu faire ce rêve. Je sais aussi que je n’ai pas pu songer à imiter ces élèves du lycée de Nevers qui, vers 1900, inventaient les rêves les plus étranges, parce que leur professeur, qui préparait une thèse sur le rêve, avait trouvé un moyen très efficace pour récompenser ceux qui lui racontaient [p. 173] leurs rêves. Enfin, si j’avais voulu le faire, je n’aurais pas imaginé un rêve qui semble contredire mes idées sur ce sujet.
D’ailleurs il ne les contredit pas absolument. J’ai insisté, en le racontant, sur le fait qu’il n’est que l’application à une figure nouvelle d’un mode de raisonnement qui m’était familier. Or il m’est parfois arrivé de voir, en rêve des dessins bien plus complexes ; il m’est arrivé par exemple, dans un demi-sommeil où l’observateur éveillé et surpris se superposait au rêveur, de voir se dérouler des paysages variés, dont le dessin et les couleurs étaient d’une netteté et d’une intensité surprenantes. Ces rêves si nets, et notamment mon rêve mathématique, restent en tout cas l’exception ; la règle, au moins depuis que j’ai dépassé trente ans, est que le rêve est un ensemble d’impressions confuses, ayant souvent pour cause une gêne du corps, et qu’il s’efface bien vite du souvenir, comme un dessin sur des sables mouvants, et cela même si au moment du réveil on cherche à le fixer dans sa mémoire. Mais qu’un rêve qui avait suffisamment retenu mon attention pour que je le note par écrit ait à ce point disparu de mes souvenirs est assez singulier et méritait d’être signalé.
Paul Lévy.
Notes
(1) Cette courbe peut notamment être une parabole de sommet O ; je crois que dans mon rêve elle était restée indéterminée.
(2) Par contre, il ne saurait être question de comparer les impressions de deux êtres différents. Peut-être même l’impression de durée que fait une seconde n’est-elle pas la même pour l’enfant et pour l’adulte. Ce qui me paraît devoir être exclu, c’est l’idée d’une variation si brusque de cette impression qu’un bruit se répétant de seconde en seconde puisse donner l’impression d’une cadence brusquement changée.
LAISSER UN COMMENTAIRE